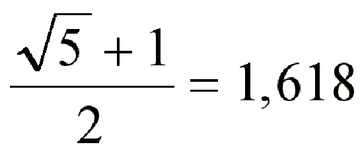
Altın oran kaşı nasıl ölçeriz, hangi yöntemler var?
Altın oran, matematikte estetik dengeyi temsil eden önemli bir orandır. Antik Yunan'dan günümüze sanatçılar ve tasarımcılar tarafından kullanılmış, doğada ve mimaride sıkça karşılaşılmıştır. Bu yazı, altın oranı ve ölçüm yöntemlerini detaylı bir şekilde ele alarak okuyuculara bilgi sunmaktadır.
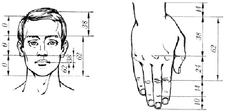
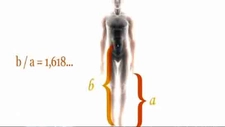
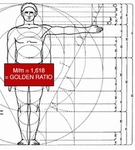
Altın Oran Nedir?Altın oran, matematiksel bir oran olup, genellikle "phi" (ϕ) sembolü ile gösterilir ve yaklaşık olarak 1.6180339887... sayısına eşittir. Bu oran, a/b = (a+b)/a eşitliği ile tanımlanır; burada a ve b pozitif reel sayılardır. Altın oran, doğada, sanatta ve mimaride sıkça karşımıza çıkan bir orandır ve estetik bir denge sağladığı düşünülmektedir. Altın Oranın TarihçesiAltın oranın kökenleri, Antik Yunan dönemine kadar uzanmaktadır. Bu oran, özellikle Euclid'in "Elementler" adlı eserinde yer almakta ve matematiksel olarak tanımlanmaktadır. Rönesans döneminde sanatçılar ve bilim insanları bu oranı eserlerinde kullanarak, estetik bir denge sağlamışlardır. Leonardo da Vinci, Michelangelo ve Le Corbusier gibi ünlü isimler, çalışmalarında altın oranı kullanmışlardır. Altın Oranın Ölçülmesi YöntemleriAltın oranı ölçmek için çeşitli yöntemler bulunmaktadır. Bu yöntemler arasında en yaygın olanları şunlardır:
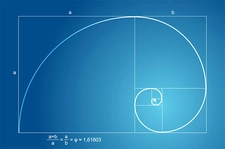
Geometrik YöntemlerGeometrik yöntemler, altın oranın ölçülmesinde en eski ve en yaygın kullanılan yöntemlerdendir. Bu yöntemde, bir dikdörtgen oluşturulur ve bu dikdörtgenin uzunluk ve genişlik oranı altın oranı sağlamalıdır.
Matematiksel HesaplamalarAltın oranı ölçmek için matematiksel hesaplamalar da yapılabilir. Bu hesaplamalar, genellikle şu formülle gerçekleştirilir:
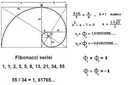
Fibonacci Dizisi KullanımıFibonacci dizisi, her sayının kendisinden önceki iki sayının toplamı olduğu bir dizidir. Bu dizi, altın oran ile güçlü bir ilişkiye sahiptir. Diziye göre, 0, 1, 1, 2, 3, 5, 8, 13, 21,... şeklinde devam eder.
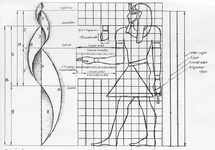
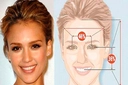
Oranların TasarımıAltın oran, tasarım ve mimaride kullanılmakta olan bir diğer önemli ölçümdür. Bu oran, mimari yapılar, grafik tasarımlar ve diğer sanatsal eserlerde estetik bir denge sağlamak için kullanılmaktadır.
SonuçAltın oran, matematiksel bir kavram olmanın ötesinde, sanat, mimari ve doğada estetik bir denge sağlamak için önemli bir araçtır. Geometrik yöntemler, matematiksel hesaplamalar, Fibonacci dizisi ve tasarım alanında kullanımı, bu oranın ne kadar yaygın ve etkili olduğunu göstermektedir. Altın oranı ölçmek ve uygulamak, yaratıcı süreçlerde önemli bir rol oynamaktadır ve bu nedenle, hem sanatçılar hem de tasarımcılar için vazgeçilmez bir araçtır. Bu makale, altın oran kavramını ve ölçüm yöntemlerini detaylı bir şekilde ele alarak, okuyuculara bu konu hakkında derinlemesine bilgi sunmayı amaçlamaktadır. |

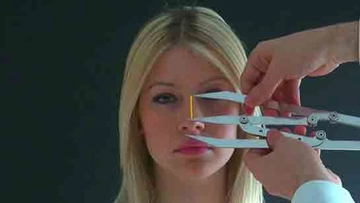

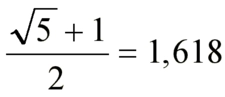

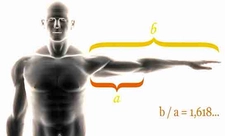

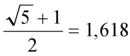


Altın oranı keşfettiğinizde, hayatın birçok alanında ne kadar etkili bir kavram olduğunu anlamak zor olmuyor. Örneğin, mimaride ve sanatta bu oranın nasıl kullanıldığını görmek, gerçekten ilham verici değil mi? Özellikle Leonardo da Vinci ve Michelangelo gibi büyük ustaların eserlerinde altın oranı nasıl uyguladıklarını düşündüğümüzde, bu oranı kullanarak estetik bir denge sağlamak ne kadar önemli bir beceri. Geometrik yöntemlerle altın oranı ölçmenin en eski yöntemlerden biri olduğunu öğrendiğinizde, bu yöntemin basit ama etkili olduğu dikkat çekiyor. Ayrıca, Fibonacci dizisinin bu oranla olan ilişkisi de oldukça ilginç. Dizideki ardışık sayıların oranının altın orana yaklaştığını görmek, doğanın matematiksel güzelliğini bir kez daha gözler önüne seriyor. Tasarımlarınızda altın oranı kullanmanın görsel hiyerarşi oluşturmada nasıl yardımcı olduğunu düşünmek bile yaratıcı süreçlerinizi geliştirebilir. Peki, siz altın oranı kendi çalışmalarınıza nasıl entegre ediyorsunuz?
Hilmi Bey, altın oranın evrensel estetikle bu denli uyumlu olması gerçekten büyüleyici. Mimari ve sanattaki örneklerini incelerken, insanın doğuştan bu orana yatkın bir algısı olduğunu hissediyor insan. Da Vinci'nin Vitruvius Adamı'nda veya Michelangelo'nun Davut heykelindeki oransal mükemmellik, bu kavramın sadece matematiksel bir formül olmadığını gösteriyor.
Geometrik Yöntemler konusundaki tespitinize katılıyorum. Cetvel ve pergel kullanarak φ değerine ulaşabilmek, antik dönemlerdeki matematiksel zekânın ne kadar ileri seviyede olduğunu kanıtlıyor. Özellikle Parthenon Tapınağı'nın tasarımında bu yöntemlerin izlerini görmek mümkün.
Fibonacci Bağlantısı ise beni her defasında şaşırtıyor. Ayçiçeği tohumlarındaki spiral dizilimden tutun, ağaç dallarının büyüme modeline kadar doğanın bu matematiği içselleştirmesi, sanırım en çok da tasarımcılara ilham veriyor.
Kendi çalışmalarımda altın oranı şu şekilde kullanıyorum:
- Kompozisyon Düzeni: Görsel ağırlık merkezlerini 1:1.618 oranına göre konumlandırıyorum
- Tipografi: Yazı puntosu ve satır aralıklarında altın oranı referans alıyorum
- Renk Dağılımı: Tasarımlarda renk bloklarının oransal dağılımını bu sisteme göre planlıyorum
Sizin de belirttiğiniz gibi, bu oranı kullanmak yalnızca estetik kaygılardan öte, izleyicide doğal bir rahatlık hissi yaratıyor. Sizin hangi alanlarda bu orandan faydalandığınızı merak ediyorum.