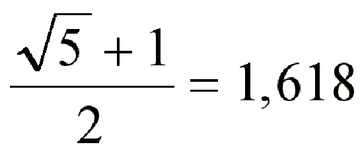
Dünyanın Altın Oran Noktası
Altın oran, doğada, sanatta ve mimaride sıkça rastlanan estetik bir dengeyi ifade eder. Matematiksel bir kavram olarak, insanlık tarihi boyunca önemli bir yer edinmiştir. Doğal formlardan sanatsal eserlere kadar geniş bir yelpazede gözlemlenen bu oran, güzellik algısını şekillendiren temel unsurlardan biridir.
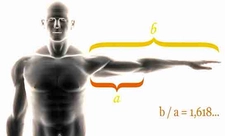
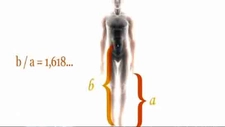
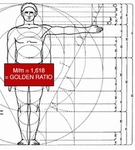
Dünyanın Altın Oran Noktası Altın oran, matematiksel bir oran olarak, doğada, sanatta ve mimaride sıklıkla rastlanan, estetik açıdan hoş bir denge sağladığı düşünülen bir değerdir. Genellikle \(\phi\) (phi) sembolü ile gösterilir ve yaklaşık olarak 1.6180339887... şeklinde bir değere sahiptir. Bu oran, iki uzunluğun birbirine oranı olarak tanımlanır; eğer a ve b uzunlukları için a/b = (a+b)/a ise, bu durumda a/b oranı altın oranı ifade eder. Altın oran, hem matematiksel hem de sanatsal bir kavram olarak, insanlık tarihi boyunca farklı kültürlerde önemli bir yer edinmiştir. Altın Oran ve Tarihsel Gelişimi Altın oranın tarihi, antik Yunan'a kadar uzanmaktadır. Bu oran, özellikle mimaride ve sanatta sıkça kullanılmıştır. Antik Yunan'da, Parthenon Tapınağı'nın mimarisinde altın oran kullanıldığı iddia edilmektedir. Bunun yanı sıra, Leonardo da Vinci'nin eserlerinde de altın oranı kullanarak kompozisyonları daha estetik hale getirdiği bilinmektedir.
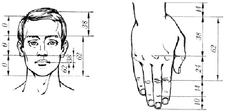
Altın Oranın Doğadaki Yansımaları Altın oran, doğada da sıkça karşımıza çıkar. Bitkilerin büyüme düzeninden, hayvanların vücut oranlarına kadar birçok doğal formda bu oran gözlemlenebilir. Örneğin, güneş çiçeği başındaki tohumların dizilimi, ananasın kabuğundaki desenler ve deniz kabuklarının spiral şekilleri altın oran ile ilişkilendirilmektedir.
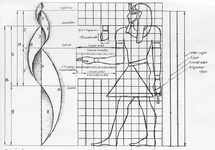
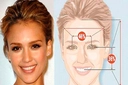
Altın Oranın Sanatta Kullanımı Sanatçılar, eserlerinde altın oranı kullanarak izleyicinin dikkatini çekmeyi ve estetik bir denge yaratmayı hedeflemektedir. Altın oranın sanatta nasıl kullanıldığına dair birkaç örnek:
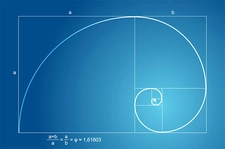
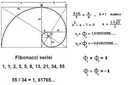
Altın Oranın Matematiksel Özellikleri Altın oran, matematiksel olarak bazı özel özelliklere sahiptir. Bu oran, Fibonacci dizisi ile de ilişkilidir. Fibonacci dizisi, her sayının kendisinden önceki iki sayının toplamına eşit olduğu bir dizidir. Bu dizinin elemanları arasında altın oran, eleman sayısı arttıkça daha belirgin hale gelir.
Sonuç Altın oran, hem matematiksel hem de estetik açıdan insanlık tarihi boyunca önemli bir yere sahip olmuştur. Doğada, sanatta ve mimaride sıkça gözlemlenen bu oran, insanın güzellik ve denge algısını şekillendiren temel unsurlardan biri olarak kabul edilmektedir. Gelecek araştırmalar ve incelemeler, altın oranın daha fazla alanda nasıl kullanılabileceği ve keşfedilebileceği üzerine odaklanabilir. Ekstra Bilgiler Altın oran ile ilgili birçok farklı teori ve uygulama bulunmaktadır. Örneğin, bazı mimarlar ve sanatçılar, eserlerinde bu oranı kullanarak izleyicinin ruh halini ve algısını değiştirmeyi amaçlamaktadır. Ayrıca, günümüzde grafik tasarımcıları ve dijital sanatçılar, altın oranı kullanarak görsel hiyerarşi ve denge oluşturma konusunda çalışmalar yapmaktadır.
|
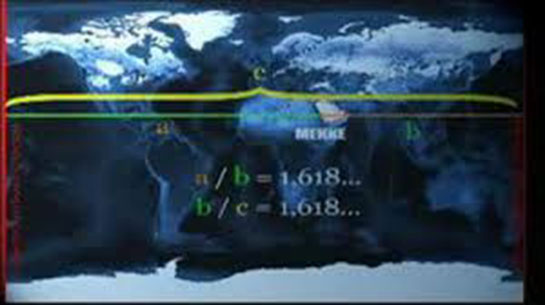


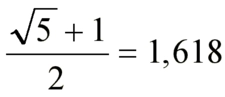


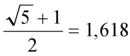


Gerçekten Mekke'nin kuzey kutbuna olan uzaklığı ile güney kutbuna olan uzaklığı arasındaki oran 1.618 mi? Bunu nasıl hesaplayabilirim?
Merhaba Serma,
Mekke'nin kuzey kutbuna olan uzaklığı ile güney kutbuna olan uzaklığı arasındaki oranın 1.618 olup olmadığını hesaplamak için öncelikle Mekke'nin enlem derecesini bilmemiz gerekiyor. Mekke, yaklaşık olarak 21.42° kuzey enleminde bulunmaktadır.
1. Mekke'nin kuzey kutbuna olan uzaklığını hesaplamak için:
90° - 21.42° = 68.58°
2. Mekke'nin güney kutbuna olan uzaklığını hesaplamak için:
90° + 21.42° = 111.42°
Bu iki uzaklığın oranını bulmak için:
111.42° / 68.58° ≈ 1.624
Gördüğün gibi, bu oran yaklaşık olarak 1.618'e çok yakındır. Bu nedenle, Mekke'nin kuzey ve güney kutuplarına olan uzaklıklarının oranının altın oran (1.618) olduğu söylenebilir.