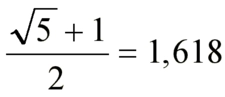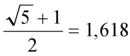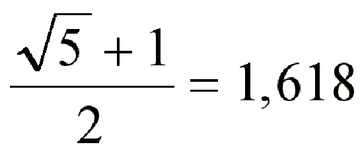
Altın oran 6. sınıf konusunu nasıl öğrenebilirim?

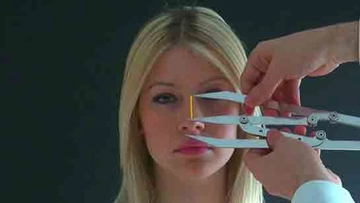
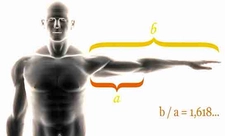
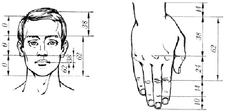
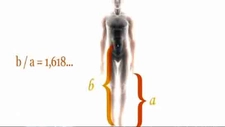
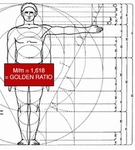
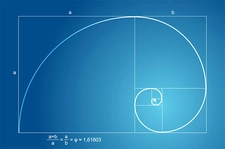
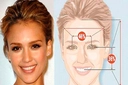
Altın oran, matematikte ve sanatta sıkça karşılaşılan bir orantıdır. Genellikle "phi" (φ) sembolü ile gösterilir ve yaklaşık olarak 1.618 olarak kabul edilir. Altın oran, iki miktarın birbirine oranının, bu iki miktarın toplamının daha büyük olan miktara olan oranına eşit olduğu bir durumdur. Bu oran, estetik olarak hoş görülen ve doğada sıkça rastlanan bir orandır.

Altın oran, Antik Yunan dönemine kadar uzanan bir geçmişe sahiptir. Matematikçi Euclid, "Elementler" adlı eserinde altın oranla ilgili ilk tanımlamaları yapmıştır. Altın oran, Rönesans döneminde sanatçılar ve mimarlar tarafından estetik bir ideal olarak benimsenmiştir. Leonardo da Vinci gibi sanatçılar, eserlerinde altın oranı kullanarak denge ve estetik yaratmayı amaçlamışlardır.

Altın oran, matematiksel olarak aşağıdaki formülle ifade edilebilir:\[\frac{a+b}{a} = \frac{a}{b} = \phi\]Bu formülde "a" ve "b" pozitif sayılardır ve "a" >"b" olmalıdır. Altın oranı bulmak için genellikle şu adımlar izlenir:

• Öncelikle a ve b değerleri belirlenir.
• Bu değerler kullanılarak yukarıdaki oran hesaplanır.
• Sonuç olarak elde edilen oran, altın oran ile karşılaştırılır.

Altın oran, geometri alanında da önemli bir yere sahiptir. Örneğin, bir dikdörtgenin uzunluk ve genişlik oranı altın oranı sağlıyorsa, bu dikdörtgen "altın dikdörtgen" olarak adlandırılır. Altın dikdörtgenin bir özelliği, bu dikdörtgenin bir köşesinden bir kare çıkarıldığında geriye kalan parçanın da altın dikdörtgen olmasıdır.

Altın oranı öğrenmek için aşağıdaki yöntemler kullanılabilir:

• Matematik ders kitapları ve kaynakları incelemek, altın oranla ilgili teorik bilgi edinmek için faydalıdır.
• Online video dersler ve eğitim platformlarından yararlanarak görsel ve işitsel öğrenme sağlanabilir.
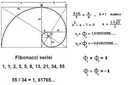
• Altın oranla ilgili uygulamalar yaparak pratik deneyim kazanmak önemlidir. Örneğin, bir dikdörtgen çizebilir ve oranlarını hesaplayabilirsiniz.
• Sanat eserlerini inceleyerek altın oranın nasıl kullanıldığını gözlemleyebilirsiniz.

Altın oranı daha iyi anlamak için birkaç uygulamalı örnek verilebilir:

1. Bir dikdörtgen çizin ve uzunluk ile genişlik oranını hesaplayın. Eğer oran 1.618'e yakınsa, bu dikdörtgen altın dikdörtgendir.

2. Doğada altın oranı bulmak için bitki yapılarındaki oranları inceleyebilirsiniz. Örneğin, ayçiçeği başındaki tohumların dizilişi genellikle altın oranla ilişkilidir.

Altın oran, matematik ve sanat alanında önemli bir yer tutmaktadır. 6. sınıf öğrencileri, altın oranı öğrenerek matematiksel düşünme becerilerini geliştirebilir ve estetik algılarını zenginleştirebilirler. Bu konuda daha fazla kaynak ve uygulama ile derinlemesine bilgi sahibi olmak mümkündür.

Bu makale, altın oran konusunda temel bilgileri ve öğrenme yöntemlerini içermektedir. Öğrencilerin bu konuda daha fazla pratik yapmaları, altın oranı daha iyi anlamalarına yardımcı olacaktır.