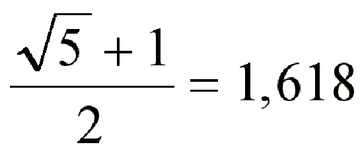
Papatya altın oran nedir ve nasıl hesaplanır?
Papatya altın oran, doğanın estetik dengesini temsil eden bir matematiksel kavramdır. Bu yazıda, papatya çiçeği üzerinden altın oranın tanımı, hesaplanması ve doğadaki önemi ele alınarak, doğal yapıların matematiksel güzellikleri incelenecektir.
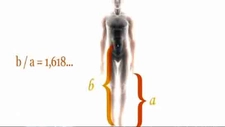
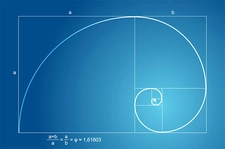
Papatya Altın Oran Nedir ve Nasıl Hesaplanır?Papatya altın oran, doğada sıkça karşılaşılan ve birçok estetik öğede temel alınan bir matematiksel kavramdır. Altın oran, sanat, mimari ve doğada bulunan birçok yapının estetik değerini belirleyen bir orandır. Papatya çiçeği, özellikle yapısında altın oranı barındırması nedeniyle bu kavramla özdeşleşmiştir. Bu makalede, papatya altın oranın ne olduğu, nasıl hesaplandığı ve doğadaki önemi üzerinde durulacaktır. Altın Oranın TanımıAltın oran, matematiksel olarak, iki sayı arasında özel bir orandır. Bu oran, \(\phi\) (phi) sembolü ile gösterilir ve yaklaşık olarak 1.618'e eşittir. İki sayı \(a\) ve \(b\) (burada \(a >b\)) için altın oran, aşağıdaki eşitlikle tanımlanır:\[\frac{a+b}{a} = \frac{a}{b} = \phi\]Bu oran, birçok doğal ve sanatsal yapıda estetik bir denge oluşturur ve göz alıcı bir görünüm sağlar. Papatya Çiçeğinde Altın OranPapatya çiçeği, yapısında altın oranı barındıran doğal bir örnektir. Bir papatya çiçeğinin merkezindeki disk çiçeklerinin düzeni, altın oran ile uyumlu bir şekilde yerleştirilmiştir. Papatyanın yaprakları ve petalleri de bu orana dayanarak düzenlenmiştir. Papatya çiçeklerinin bu özelliği, doğanın estetik ve simetrik düzeninin bir yansımasıdır. Altın Oranın HesaplanmasıPapatya altın oranını hesaplamak için aşağıdaki adımlar izlenebilir:
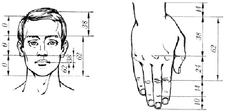
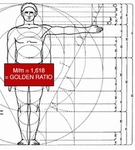
Altın Oranın Doğadaki ÖnemiAltın oran, doğada birçok yapıda ve organizmada gözlemlenmektedir. Bu oran, bitkilerin büyüme düzeninden, hayvanların vücut oranlarına kadar geniş bir yelpazede karşımıza çıkar. Doğal sistemlerin dengesi ve estetiği açısından altın oran, ekosistemin sağlıklı işleyişine katkıda bulunur. Ayrıca, sanat ve mimaride kullanılan altın oran, insan gözünde hoş bir estetik algısı yaratır ve bu nedenle özellikle ressamlar ve mimarlar tarafından sıklıkla tercih edilir. SonuçPapatya altın oran, doğanın matematiksel ve estetik düzeninin bir parçasıdır. Bu oranı hesaplamak, doğayı daha iyi anlamamıza ve estetik olanla olan ilişkilerimizi keşfetmemize yardımcı olur. Papatya gibi doğal öğelerin altın oranı barındırması, doğanın ne kadar mükemmel bir dengeye sahip olduğunu ortaya koymaktadır. Doğadaki bu matematiksel düzenin anlaşılması, hem bilimsel hem de sanatsal alanlarda önemli bir yer tutmaktadır. Bu makalede, papatya altın oranı üzerine kapsamlı bir inceleme yapılarak, hem teorik hem de pratik bilgiler sunulmuştur. Altın oranın doğadaki ve sanattaki yeri, insanlık tarihi boyunca merak edilen ve araştırılan bir konu olmuştur. |


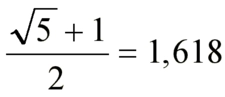

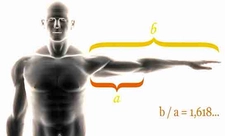

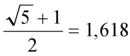


Papatya altın oranını duyduğumda, doğanın içinde bu kadar matematiksel bir düzenin olduğunu düşünmek oldukça ilginç geliyor. Bu oranı hesaplamak için papatya çiçeğinin merkezindeki disk çiçeklerinin sayısını belirlemek ve çevresindeki petal sayısıyla karşılaştırmak gerektiği bilgisi, benim gibi doğayı gözlemleyen biri için oldukça öğretici. Peki, bir papatya çiçeğinin altın oranı sağladığını anlamak için bu oranı nasıl hesapladığınızı merak ediyorum. Gerçekten de doğadaki bu estetik dengenin, sadece papatyalarla sınırlı olmadığını ve birçok bitki ve hayvan türünde de bulunduğunu öğrenmek, doğaya olan hayranlığımı artırıyor. Bu oranı keşfetmek, doğanın ne kadar mükemmel bir dengeye sahip olduğunu görmemi sağlıyor. Sizce bu matematiksel düzenin, doğadaki diğer canlılar üzerinde de benzer etkileri var mıdır?
Merhaba Aysel Hanım,
Papatyalarda altın oran hesaplaması genellikle şu şekilde yapılır:
Disk Çiçekleri ve Petal Sayısı İlişkisi:
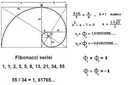
Papatyanın merkezindeki disk çiçekleri (tüp şeklindeki küçük çiçekler) spiral bir desen oluşturur. Bu spiraller saat yönünde ve tersi yönde sayıldığında, iki yöndeki spiral sayılarının oranı altın orana (yaklaşık 1.618) yakın çıkar. Örneğin, 34 ve 21 spiral sayısı bulunan bir papatyada 34/21 ≈ 1.619 değeri elde edilir.
Petal-Disk Oranı:
Bazı durumlarda, petal sayısının disk çiçeklerinin düzenine oranı da incelenir. Ancak asıl matematiksel uyum, merkezdeki Fibonacci spirallerindedir.
Doğadaki bu matematiksel düzenin diğer canlılar üzerindeki etkilerine gelirsek:
- Bitkilerde: Ayçiçeği, kozalak ve ananas gibi yapılarda benzer spiral desenler ve altın oran görülür. Bu, büyüme verimliliği ve ışık alımını optimize eder.
- Hayvanlarda: Deniz kabuklarındaki logaritmik spiraller, arı kovanlarındaki petek hücreleri veya yunusların vücut oranları gibi örnekler, doğal seleksiyonun bu dengeleri desteklediğini gösterir.
- İşlevsellik ve Estetik: Bu oranlar, dayanıklılık, enerji verimliliği veya av-avcı dinamikleri gibi faktörlerle ilişkilidir. Aynı zamanda insan algısında da estetik bir uyum yaratarak evrensel bir etkiye sahiptir.
Doğanın bu gizli matematiği, aslında tüm canlıların birbiriyle bağlantılı olduğunu ve evrimsel süreçte en uyumlu formların hayatta kaldığını hatırlatıyor. Gözlemlerinizde bu dengeleri fark etmeniz, doğaya olan bakışınızı daha da derinleştirecektir.