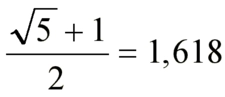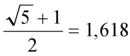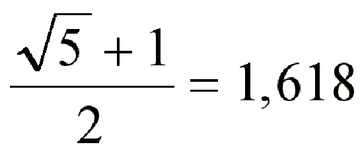
Eğrelti otu altın oranı nedir, nasıl hesaplanır?

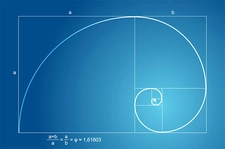
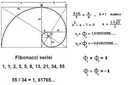
Eğrelti otları, doğadaki birçok bitki gibi büyüme ve yaprak düzenlerinde matematiksel desenler sergiler. Bu desenlerden biri, genellikle "altın oran" veya Fibonacci dizisi ile ilişkilendirilen spiral yapılardır. Eğrelti otlarının yaprakları veya sürgünleri, merkezden dışa doğru spiral bir düzen izleyerek büyür ve bu düzende altın oranın izlerini görmek mümkündür.

Altın oran (yaklaşık 1.618), matematikte ve doğada sıkça karşılaşılan bir orandır. Eğrelti otlarında bu oran, yaprakların veya dalların spiral dizilişinde ortaya çıkar. Örneğin, bir eğrelti otunun yaprakları merkezden dışa doğru büyürken, ardışık yapraklar arasındaki açı veya mesafe oranları altın orana yakın değerler gösterebilir. Bu, bitkinin ışık ve alandan en verimli şekilde yararlanmasını sağlayan bir adaptasyondur.

Eğrelti otundaki altın oranı hesaplamak için genellikle spiral diziliş analizi kullanılır. İşte temel adımlar:

Basit bir örnekle, bir eğrelti otunun spiralinde 5 turda 8 yaprak varsa, yaprak sayısı oranı 8/5 = 1.6 olur, bu da altın orana (1.618) oldukça yakındır. Benzer şekilde, açı ölçümünde 360°/1.618 ≈ 222.5° yerine, tamamlayıcı açı olan 137.5° kullanılır, çünkü bu, spiralin simetrisini korur.

Eğrelti otları, altın oranın doğadaki güzel örneklerinden biridir. Bu oran, bitkinin estetik ve fonksiyonel tasarımının bir parçasıdır. Hesaplamalar, gözlem ve matematiksel analizle yapılabilir; ancak, tüm eğrelti otları tam olarak aynı oranı göstermeyebilir, çünkü bu, türlere ve çevresel faktörlere bağlı olarak değişebilir. Doğa severler ve matematik meraklıları için bu, bitkilerin gizemli dünyasını keşfetmek için harika bir yoldur.