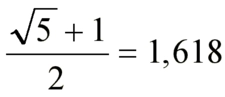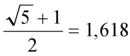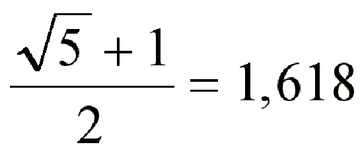
Altın oranı matematiksel olarak nasıl hesaplayabiliriz?

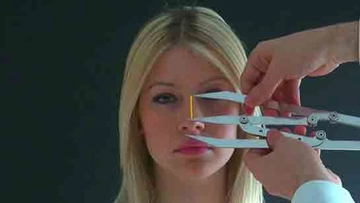
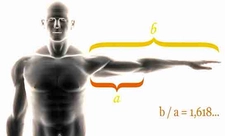
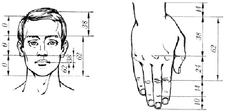
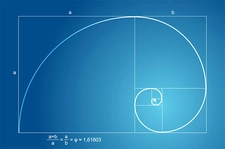
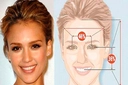
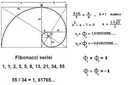
Matematiksel bir sabit olan altın oran, doğadan sanata pek çok alanda estetik dengenin temelini oluşturur. İki parçanın birbirine ve bütüne olan oranındaki bu uyum, hem geometrik hesaplamalarla hem de Fibonacci dizisi gibi doğal desenlerle açıklanabilir.

Konu kakkında 1 soru soruldu ve cevaplandı

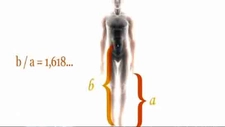
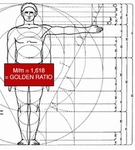
Altın Oran Nedir?

Altın oran, genellikle φ (phi) sembolüyle gösterilen ve yaklaşık olarak 1,6180339887 değerine sahip olan matematiksel bir sabittir. İki büyüklük arasındaki oran, büyük olanın küçük olana oranı, büyük ile küçüğün toplamının büyüğe oranına eşit olduğunda altın oran oluşur. Bu oran, doğada, sanatta ve mimaride sıklıkla karşımıza çıkar ve estetik açıdan hoş kabul edilir.

Altın Oranın Matematiksel Hesaplanması

Altın oranı hesaplamanın birkaç yaygın yöntemi vardır:

İki Parçalı Doğru Parçası Yöntemi: Bir doğru parçasını, uzun parçanın kısa parçaya oranının, tüm doğrunun uzun parçaya oranına eşit olacak şekilde böldüğümüzde altın oran elde edilir. Matematiksel olarak, a ve b uzunlukları için (a >b olmak üzere) a/b = (a+b)/a = φ şeklinde ifade edilir.
İkinci Dereceden Denklem Çözümü: Altın oran, φ² = φ + 1 denklemini sağlar. Bu denklemi çözdüğümüzde φ = (1 + √5)/2 sonucuna ulaşırız. Pozitif kök altın oranı verir: φ = (1 + √5)/2 ≈ 1,6180339887.
Fibonacci Dizisi ile Yaklaşım: Fibonacci dizisindeki ardışık terimlerin oranı, dizinin ilerleyen terimlerinde altın orana yakınsar. Örneğin, 5/3 ≈ 1,666..., 8/5 = 1,6, 13/8 = 1,625, 21/13 ≈ 1,615... şeklinde devam eder ve sonunda φ değerine yaklaşır.
Sürekli Kesir Gösterimi: Altın oran, φ = 1 + 1/(1 + 1/(1 + 1/(1 +...))) şeklinde sonsuz bir sürekli kesir olarak ifade edilebilir. Bu gösterim, altın oranın kendine özgü özelliklerini vurgular.

Örnek Hesaplama

Altın oranı hesaplamak için en basit yöntem, φ = (1 + √5)/2 formülünü kullanmaktır. √5 yaklaşık 2,236067977 olduğundan, φ = (1 + 2,236067977)/2 = 3,236067977/2 = 1,6180339885 olarak bulunur. Bu değer, altın oranın yüksek hassasiyetli bir yaklaşımıdır.

Altın oran, matematiksel olarak bu yöntemlerle kolayca hesaplanabilir ve birçok alanda uygulama bulur.

Yeni Soru Sor / Yorum Yap

Sizden Gelen Sorular / Yorumlar